“수학을 언제까지 옆에서 봐줘야 되지?”
  “곱셈, 나눗셈도 잘 틀리는데, 그것부터 완벽하게 해야 할 텐데...”

   아이가 어릴수록 엄마는 지금 현재 아이이 수준으로만 수학을 보려고 한다.
  간단히 풀 수 있는 문제는 놓고 대부분 그 문제에만 해당하는 설명을 하는 것으로 그치고 만다. 그러나 겉으로는 비슷해 보이나 그 속 사정은 다른 문제를 만나면 또 처음부터 다시 설명을해야 한다. 아이에게 이런 일이 반복될 경우, 스스로 원리를 이해하기는커녕 엄마의 설명에만 의존할 수 있다. 아이가 어리다고 초등학교에서만 통하는방식으로 접근하면 지금은 무사히 넘어갈 수도 있겠지만 앞으로 매번 이러한 경우가 찾아올 것이고 그때마다 아이는 좌절과 포기를 경험하게 될는지도 모른다.

  수학을 짧게만 보는 것은 수학의 단계별 연결성을 무시한 것이다. 수학은 계통학습이다. 지금 세상은 급변하고 있고, 수학교육의 흐름도 조금씩 바뀌고 있다. 부모 세대의 교육방식만을 고집하고 교육의 흐름을 놓치면 아이이 고생을 하게 된다.
  이번에 소개하는 초등 3학년 과정에는 수학과 멀어지게 하는 1차 관문인 도형이 등장한다. 가베를 활용하면 교과서 지면으로는 이해가 어렵던 도형이 입체적인 관찰로 쉽게 해결을 할 수 있다는 것을 알게 될 것이다. 그럼 도형 가분수 학습을 시작해보기로 하자!

  도형 움직이기 단원은 뒤집기와 돌리기처럼 도형을 이동시켰을때 변화된 도형의 형태를 인식하며 공간 감각을 익히는 학습내용이다.
  국어 노트나 모눈종이 위에 가베로 도형을 만들어놓고 실제로 돌리기와 뒤집기를 해보자. 90°씩 돌리는 것이 익숙지 않다면 종이의 4면을 90°로 설명하고 종이를 돌리며 원리를 이해시키도록 한다.

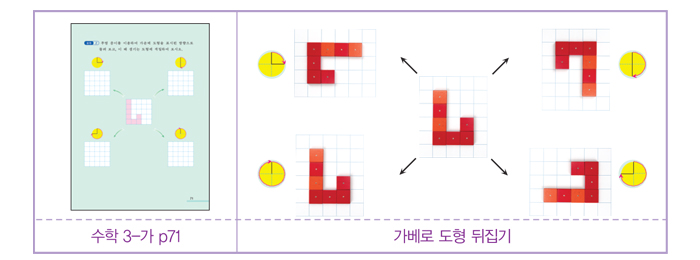
  뒤집기는 대칭의 개념이다. 대칭의 개념을 설명할 때 가장 좋은것은 거울이다.   네모난 거울을 대칭선에 대어 비치는 모습을 관찰하게 하여 이해를 돕는다.

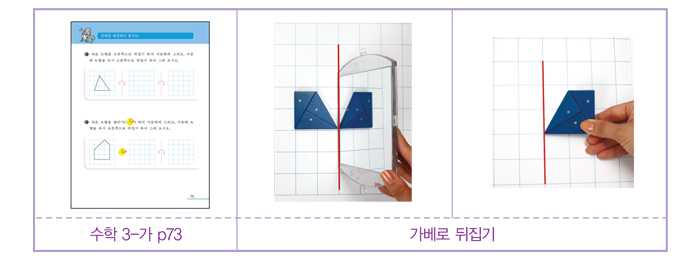
  가베로 입체도형을 만들어 뒤집기를 해본다.
  그림을 보고 대칭이 되도록 구성물을 만들 수도 있다.

  아이들이 가장 혼동하기 쉬운 것이 위·아래로 뒤집기와 180°돌리기인데, 뒤집기는 좌우의 형태가 바뀌지만 돌리기는 좌우, 상하 형태가 바뀌지 않는다. 그러나 아래와 같이복합적인 문제에서는 두 가지가 함께 이루어지므로 공간 감각이부족한 아동의 경우는 쉽사리 포기해 버리기도 한다.
  가베로 직접 도형을 만들어 돌려보면나서 체험적으로 익히도록 돕는다.

  초등학교에서 다루는 분수는 크게 전체에 대한 부분의 관계를수로 나타내는 분수, 나눗셈의 몫인 분수, 비율로서의 분수다.
  3-가 과장은 전체에 대한 부분의 관계를 나타내는 분수의 학습이다.
  그런데 왜 어렵게 느껴질까? 아이들이 혼동하기 쉬운 것은 이런 경우이다. 2/3을 3개 중의 2개라고 하면, 4/6은 6개 중의 4개가 된다. 그렇다면 2/3과 4/6의 크기는 다르다고 볼 수 있다.
한쪽은 2개이고, 또 한쪽은 4개이기 때문이다. 이런 혼동이 생기지 않으려면 분수를 1이라는 전체 크기에서 접근해야 한다.
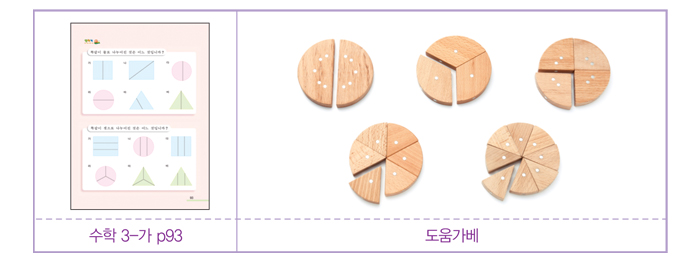
  도움가베를 사용하여 1에서 나누어 진분수의 원리를 이해하자.

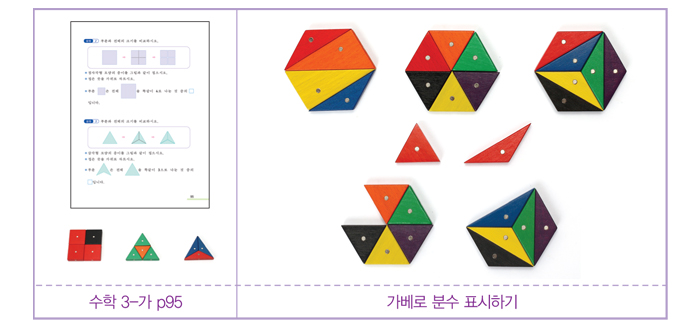
  가베로 육각형을 만들어보면 6등분된 7가베 둔각이등변삼각형과 정삼각형의 넓이는 동일하다는 것을 유추할 수 있다.

  분수에 대해 이해했다면 어떤 수의 2/3가 12일 때, 어떤 수가 얼마인지도 구할 수 있다.
   아이가 잘 이해하지 못한다면 우선 그 어떤 수가 12보다큰 수인지 아닌지를 물어본다. 제대로 대답하지 못하면 다시 분수의 이해부터 시작한다. 3등분된 분수조각을보여주며 그중 2조각의 합이 12라면 한 조각은 몇인지 물어본다. 이것이 약분의 이해이다. 이처럼 수학은 초기 과정부터 상위개념들을 포함하고 있다. 그래서 수학은 공식보다 원리를 이해해야 하는 학문이다.